用 Tensorflow 可视化梯度下降

学习资料:

• 本节代码
• 为 TF 2017 打造的新版可视化教学代码
• 什么是梯度下降4分钟短视频

要点 ¶

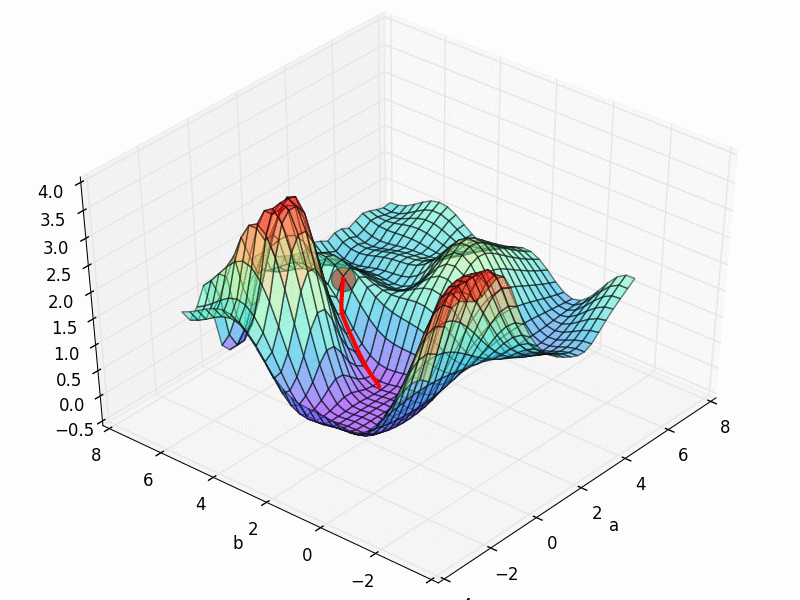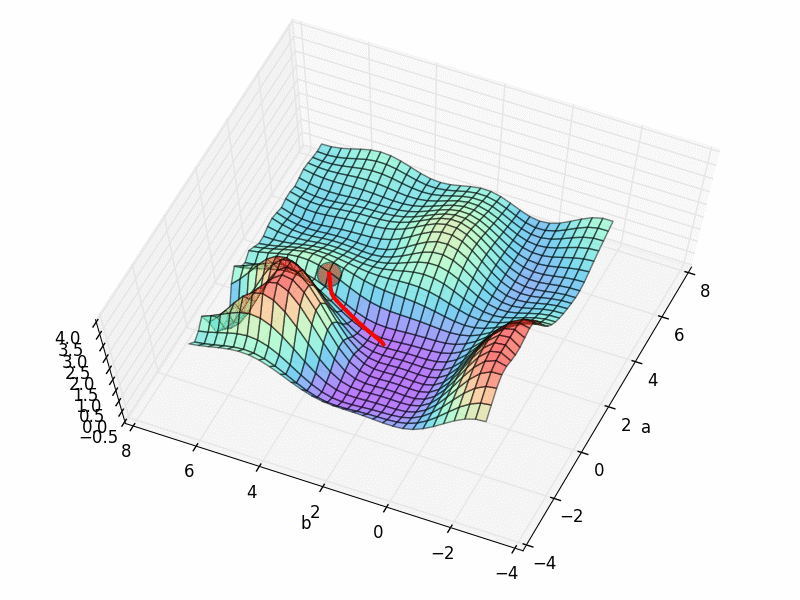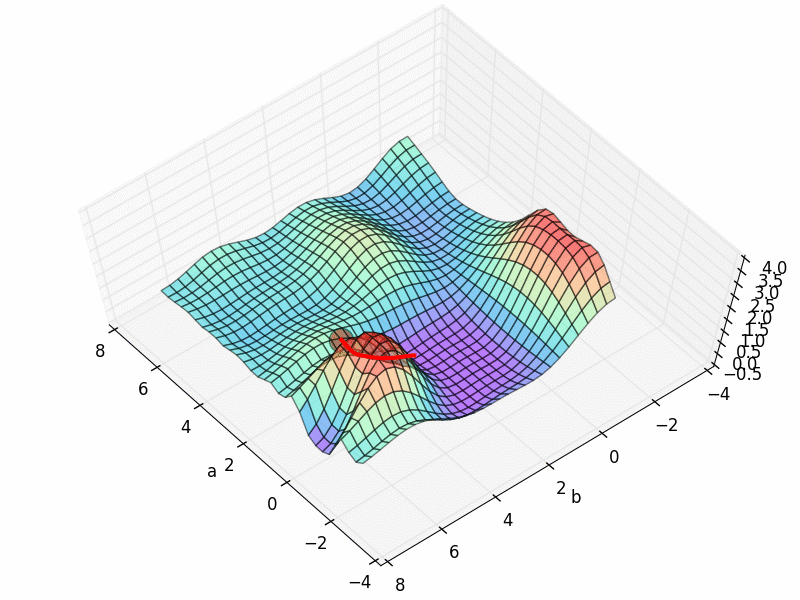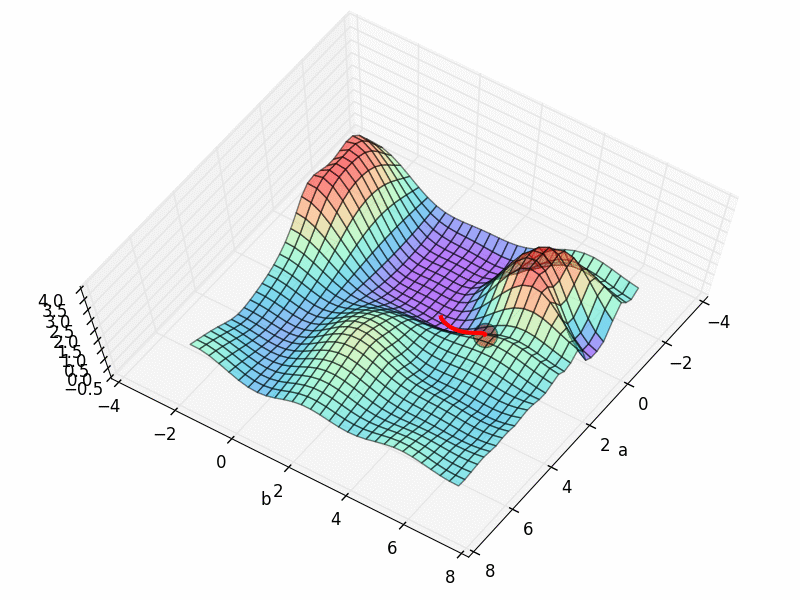
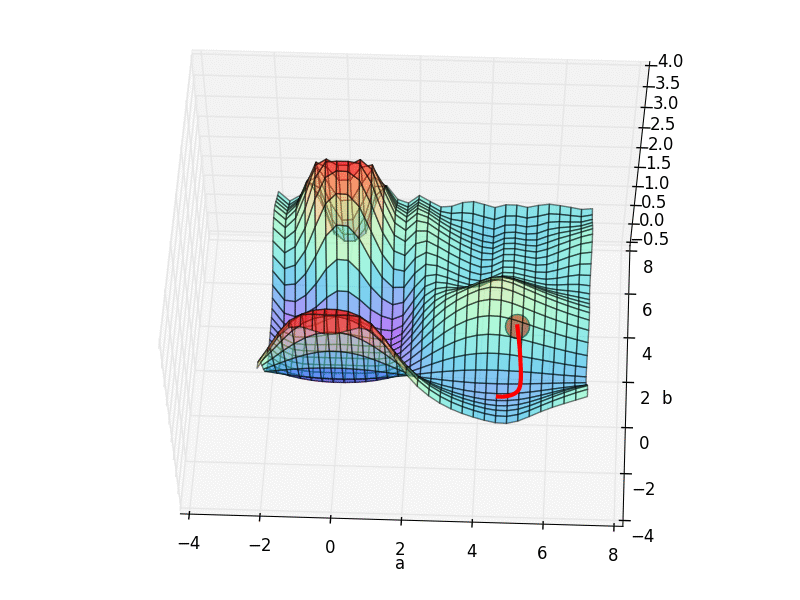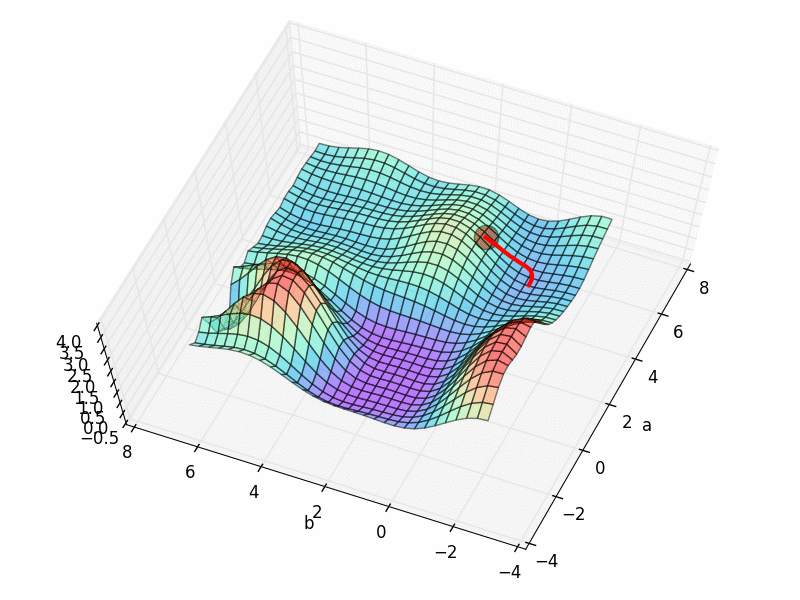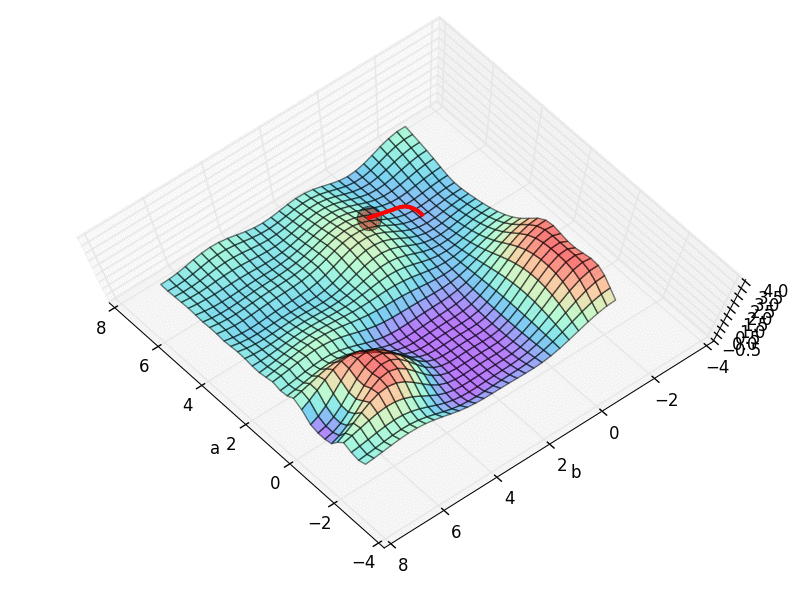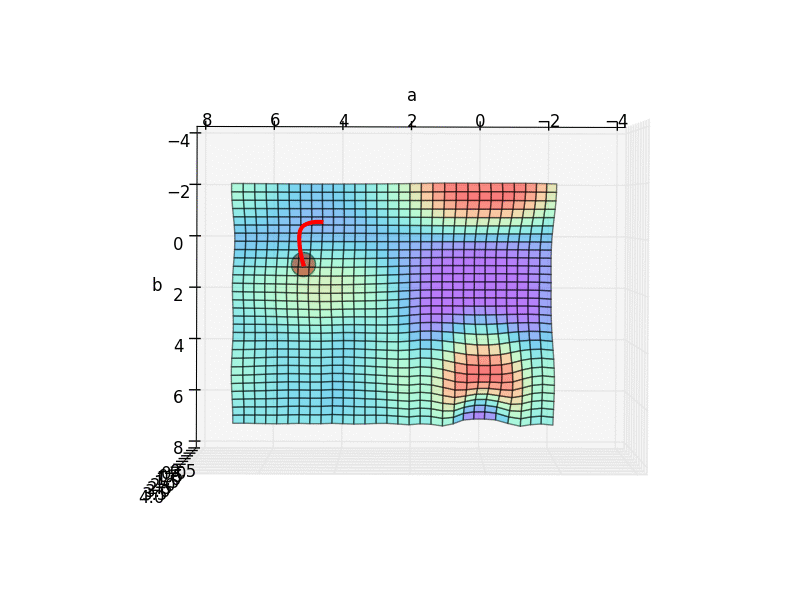
这一次, 我们想要真正意义上的看到自己手中的模型是怎么样进行梯度下降 (gradient descent) 的. 打个比方就像下面这张图. 红色圆点就是最开始的参数误差.

同时, 我们还可以扩展开来, 神经网络就是一种梯度下降的方法. 而梯度下降是一种最优化方法, 我们还能拿它来干点其它事. 比如说 为公式调参. 我们会在下面具体讲解.

接着我们还会提到在梯度下降中, 以及神经网络中很难避免的一种现象, 叫做局部最优, 以及局部最优的影响.

普通的梯度下降 ¶

这次我们还是以代码的形式直观地展示我们要做的事情. 为了可视化梯度下降的过程, 我们需要用到 Python 中的几个模块, matplotlib, numpy, tensorflow. 如果对画图感兴趣的朋友们, 可以来看看我的 python 画图教程.

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D     # 画 3D 图的功能

LR = .1     # 神经网络的学习率
REAL_PARAMS = [1.2, 2.5]    # 我们假设的需要被学习的真实参数
INIT_PARAMS = [[5, 4],      # 在调参中不同初始化的参数点
               [5, 1],
               [2, 4.5]][0]

x = np.linspace(-1, 1, 200, dtype=np.float32)   # x 数据

我们需要用 tensorflow 来帮我们梯度下降, 我们需要规定的就是最开始从哪里开始梯度下降, 这就是 INIT_PARAMS 的作用了. 我们会在之后的内容中尝试上面不同的初始化地点, 然后看看会有什么样的效果. 同时我们也会看看不同学习效率 LR 对模型学习的影响.

# test 1
y_fun = lambda a, b: a * x + b
tf_y_fun = lambda a, b: a * x + b

接着我们开始定义第一轮测试的公式. 假设我们要来拟合公式 a*x+b 中的参数 a 和 b, 我们就用 python 中的 lambda 来定义一个方程 y_fun. y_fun 的输入就是不同参数 a b 的值, 和 我们之前定义的数据 x, 输出 y 值. 这里的 tf_y_fun 是传给 tensorflow 去优化的方程. y_fun 是用来可视化和计算真是 y 用的.

noise = np.random.randn(200)/10
y = y_fun(*REAL_PARAMS) + noise         # target

所以我们就能用 y_fun 来输出 正是 y数据. 当然为了看起来真实点, 我们还加了些随机噪点.

# tensorflow 计算优化图
a, b = [tf.Variable(initial_value=p, dtype=tf.float32) for p in INIT_PARAMS]
pred = tf_y_fun(a, b)
mse = tf.reduce_mean(tf.square(y-pred))
train_op = tf.train.GradientDescentOptimizer(LR).minimize(mse)

接着我们就来定义 Tensorflow 的计算优化图纸. 定义两个参数 a, b 并给他们初始化成我们最开始假设的初始化值 INIT_PARAMS. 然后预测, 然后算误差, 最后优化.

a_list, b_list, cost_list = [], [], []
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for t in range(400):
        a_, b_, mse_ = sess.run([a, b, mse])
        a_list.append(a_); b_list.append(b_); cost_list.append(mse_)    # record parameter changes
        result, _ = sess.run([pred, train_op])                          # training

接着我们就开始训练, 并时刻记录训练时的 a,b 参数 以及 误差 变化.

最后可视化他们, 因为可视化代码不是重点, 所以想仔细看代码的朋友, 欢迎来我的 Github 中看全套代码.

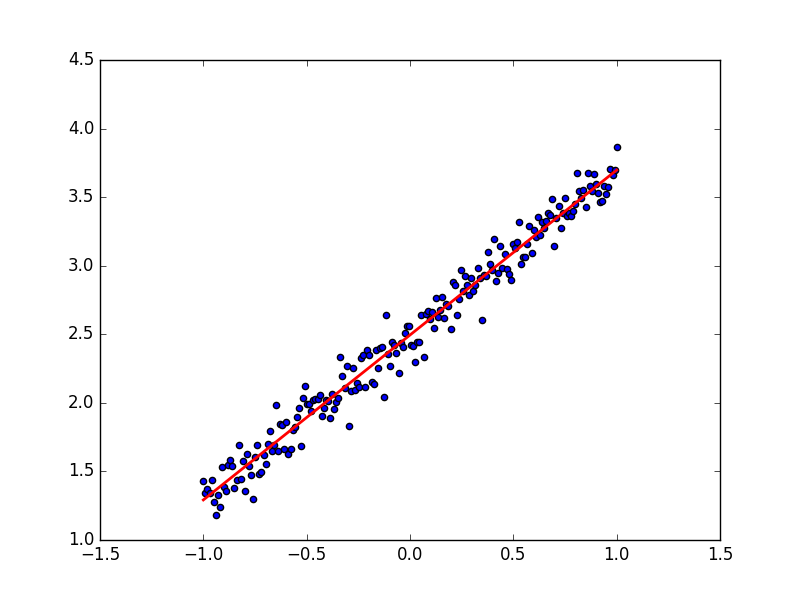
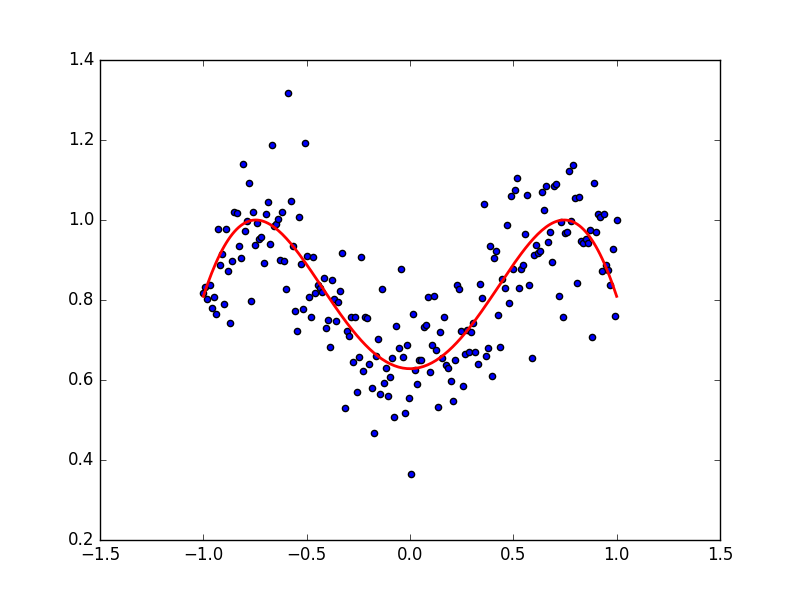
首先我们先看看训练出来的预测线和数据的拟合度吧:

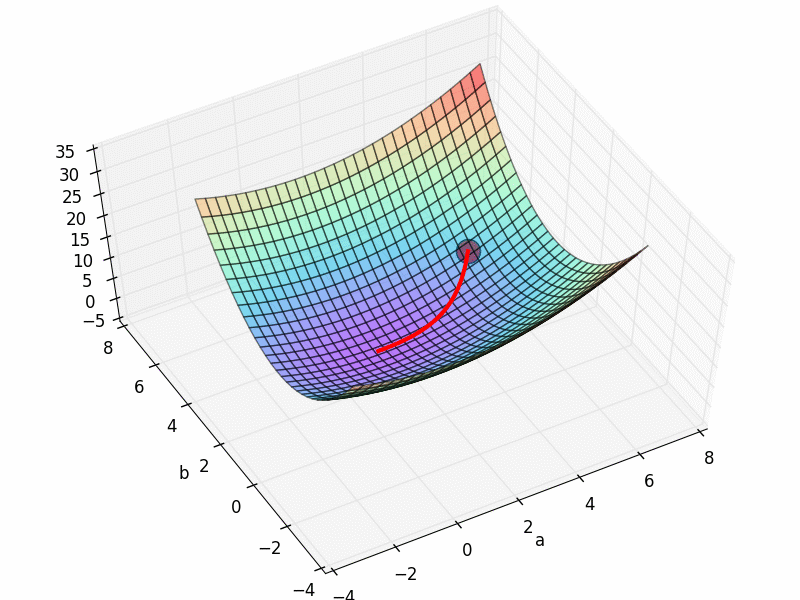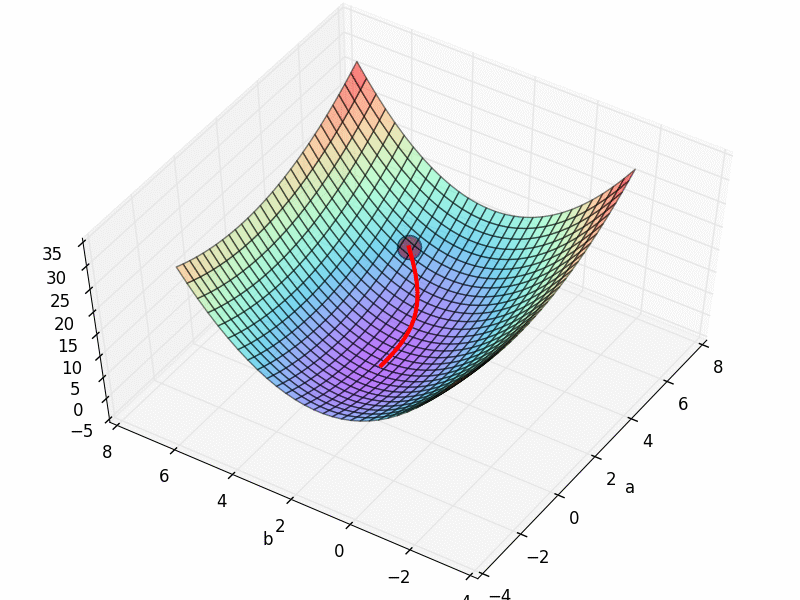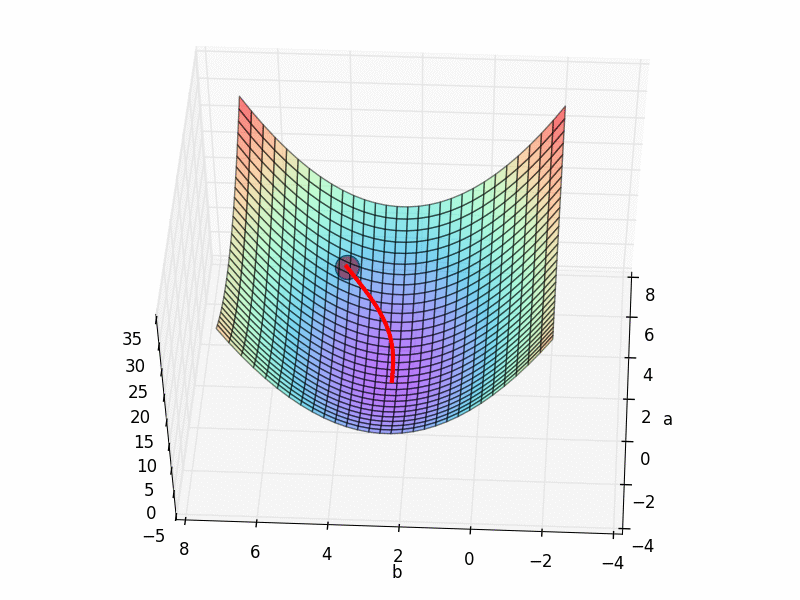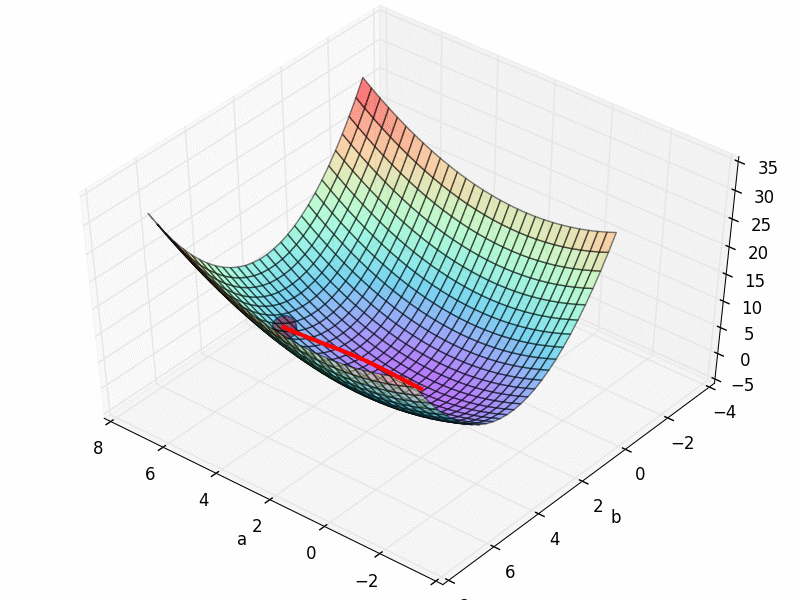
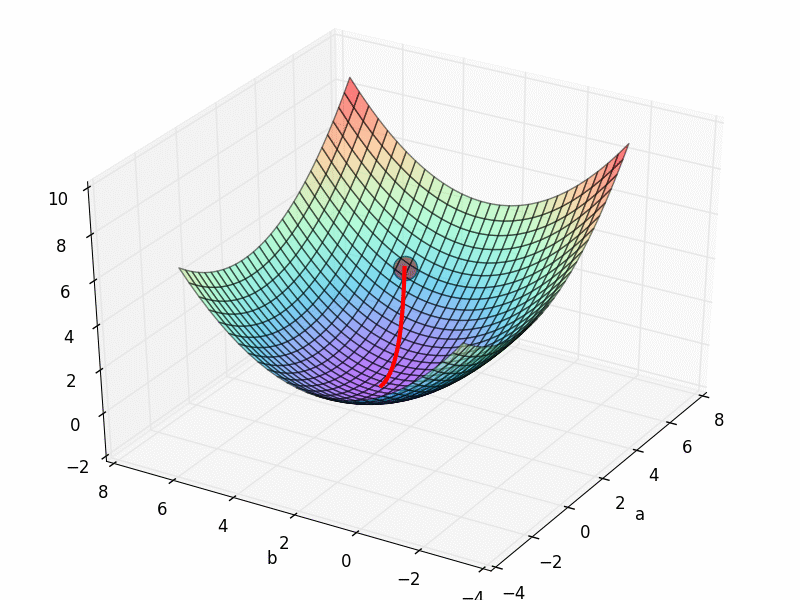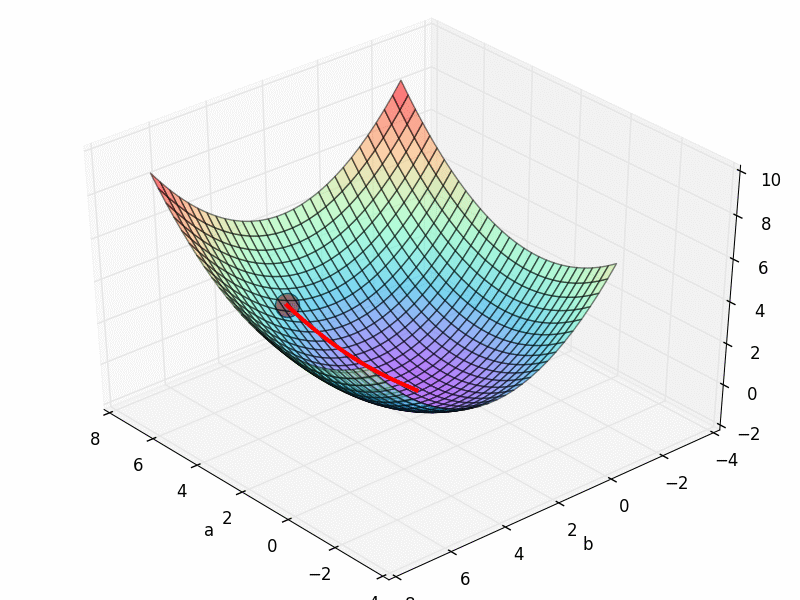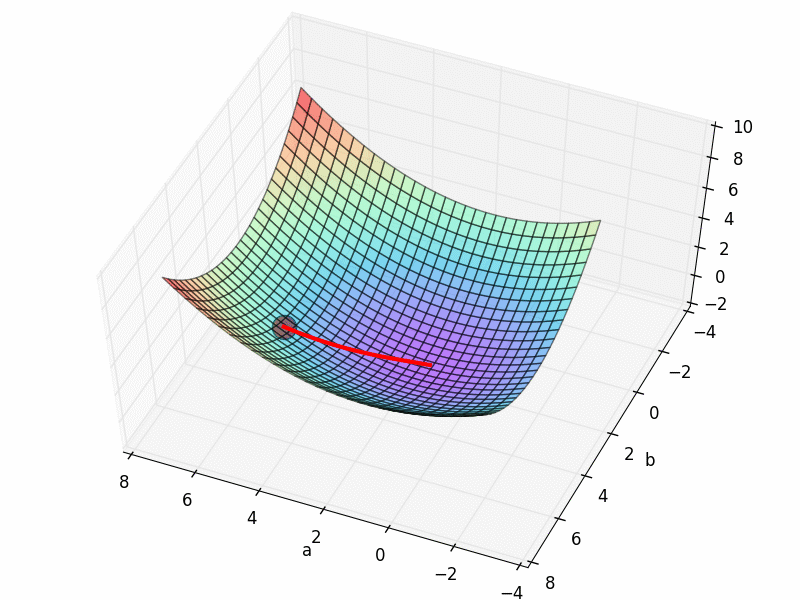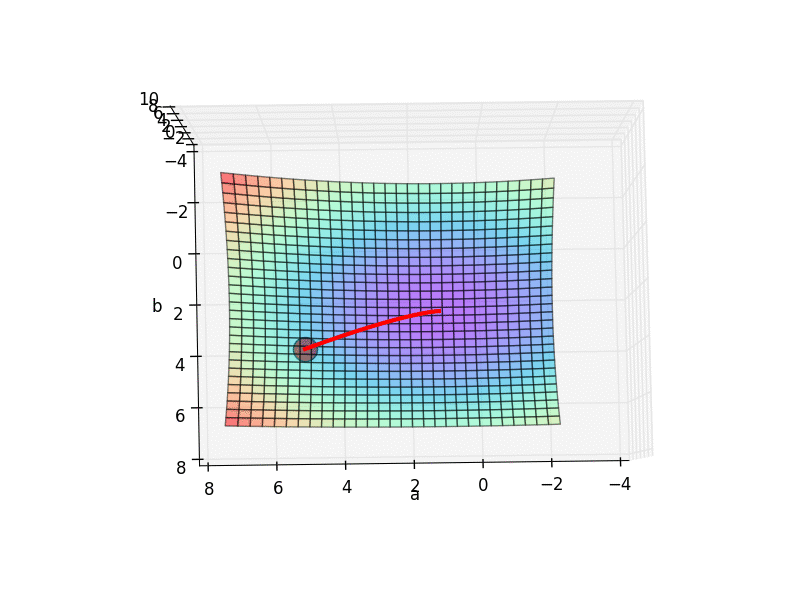
看起来非常完美, 成功的用一条直线预测出了规律. 那我们看看梯度下降的 3D 图,

看上去他从最开始的红点, 很顺利的滑落到了误差最小的地方. 梯度下降圆满完成.

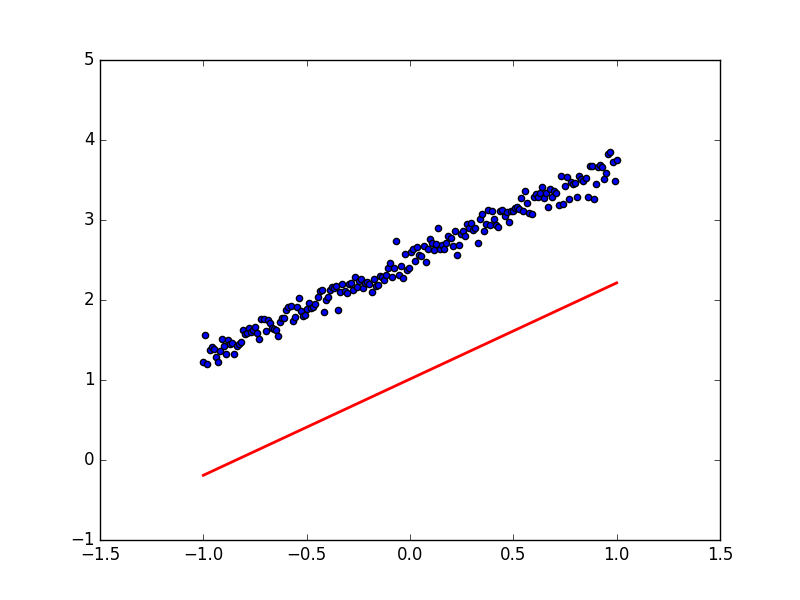
如果我们来尝试不同的学习效率呢, 比如调整最开始的 LR=1, 就会发生下面这样的事.

貌似这时的梯度下降变得纠结起来, 梯度下不去了. 原来这就是因为学习效率过大的原因, 导致虽然学得快, 但是没办法收敛. 我们也能从学习到的预测线看出来这样的现象, 现在下面的预测线没有办法预测出真实数据了. 所以切记, 当你的模型没办法收敛的时候, 试试调低学习率.

为模型,公式调参 ¶

接下来我们看看 Tensorflow 的另一种用途, 为公式调参. 说到底, 神经网络就是用梯度下降, 而梯度下降就是一种优化模式 具体参考我制作的这个短视频. 所以我们也可以使用 Tensorflow 的梯度下降机制来调参. 比如我们将上面的提到的 y_fun 和 tf_y_fun 改成下面这样 (其实上面也是在调参).

# test 2
y_fun = lambda a, b: a * x**3 + b * x**2
tf_y_fun = lambda a, b: a * x**3 + b * x**2

现在有点像一个经验公式了吧. 其实很多时候, 人们总结出来的经验公式其实是很有用的, 我们没必要大费周章来使用神经网络处理所有问题, 首先遇到一个问题, 你要想的是, 在这个问题中, 是否以前有人提出过什么经验公式的, 那我来对这个经验公式调调参. 这可比神经网络方便多了. 而且梯度下降调参只是调参中的一种方式, 还有很多种调参方式, 具体可以看看和使用 python 的另一个模块 scipy 中的 optimization 链接.

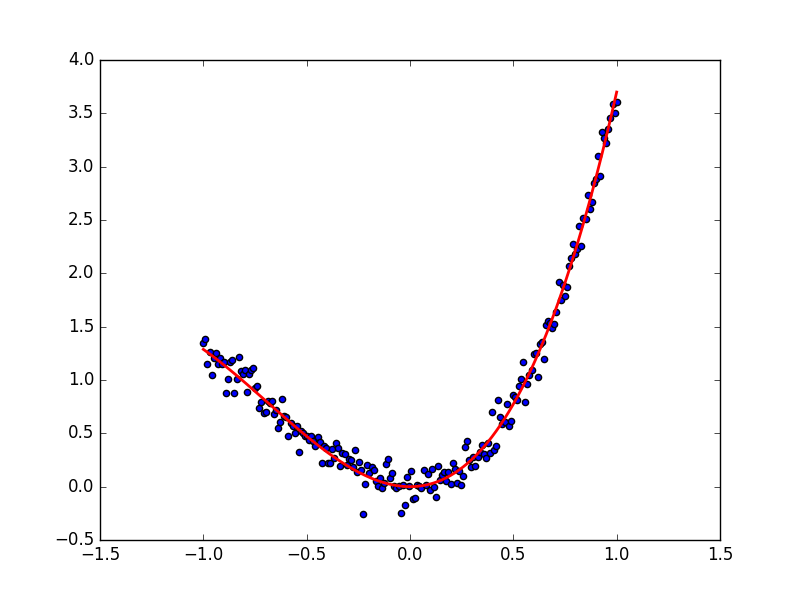
好了, 如果你决定用梯度下降调参, 这份代码就是一种途径. 代码的其他部分不用过多更改. 我们直接来看效果吧. 首先看看数据点和拟合参数a, b 后的曲线.

再来看看之前的梯度下降图:

局部最优,全局最优 ¶

在回到神经网络的话题中来, 多层的有激活神经网络必定有很多局部最优解的. 我在这个短视频中也提过什么是全局最优和局部最优. 那么我们就来做一个有两个参数的简单神经网络吧. 同样, 我们至于要修改 y_fun 和 tf_y_fun 就好了:

# test 3
y_fun = lambda a, b: np.sin(b*np.cos(a*x))
tf_y_fun = lambda a, b: tf.sin(b*tf.cos(a*x))

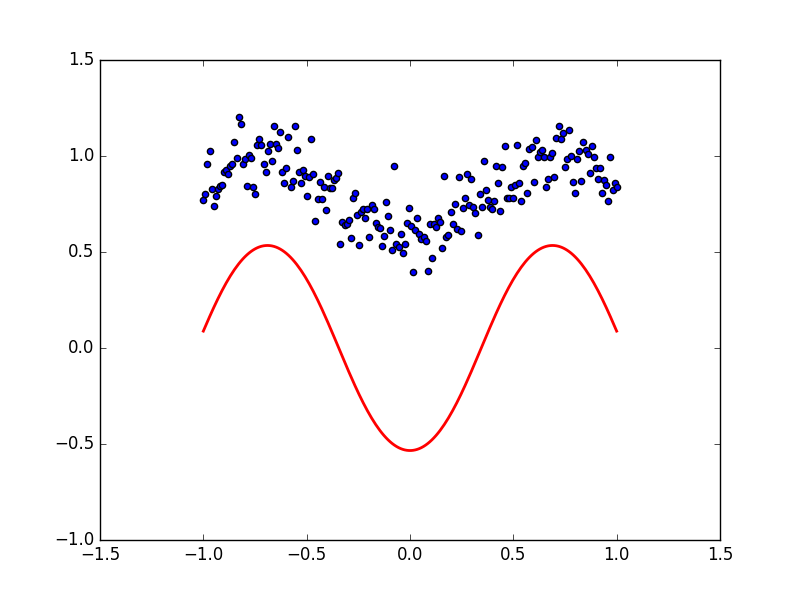
想象 np.cos(a*x) 是有激活的一层神经层, np.sin(b*last_layer) 是有激活的第二层. 那么这个方程就是最简单的一种两层神经网络了. 如果使用的初始参数点是 INIT_PARAMS=[2, 4.5] 他的数据点和拟合曲线是下面这样:

他的梯度下降空间就是我们最开始看到的那个.

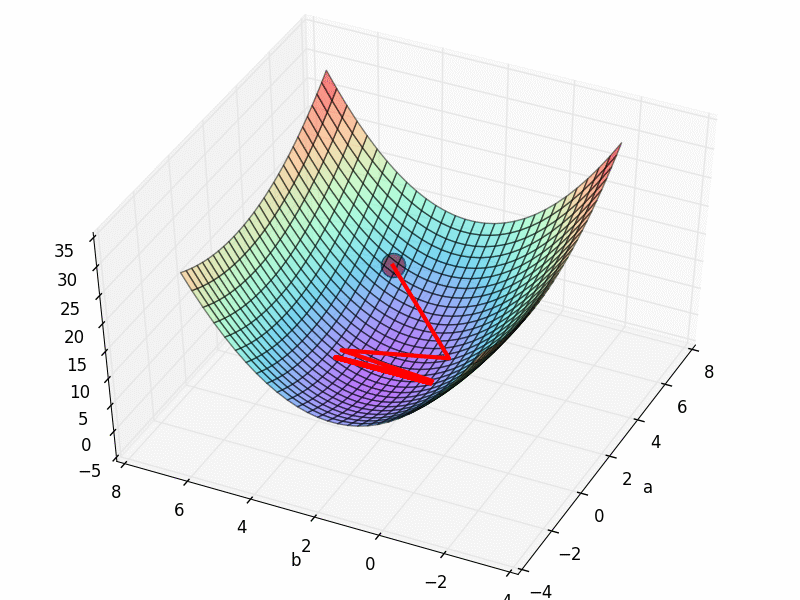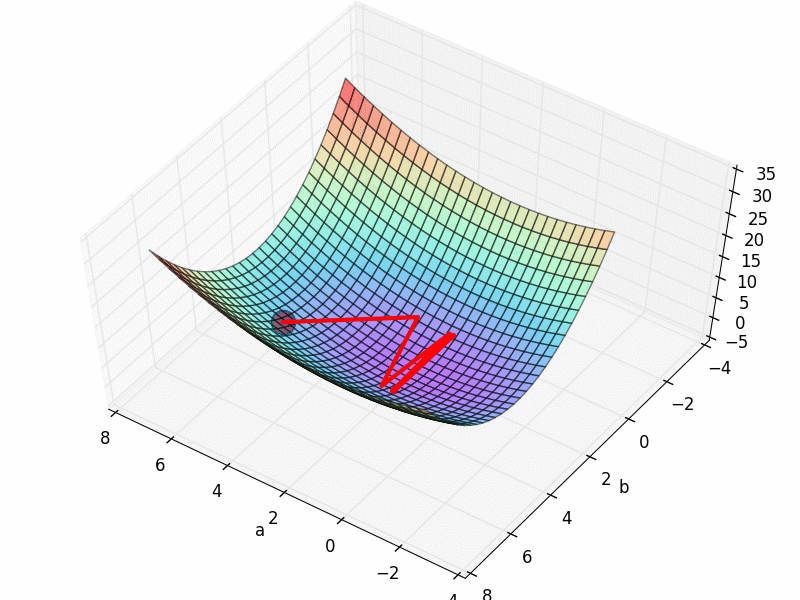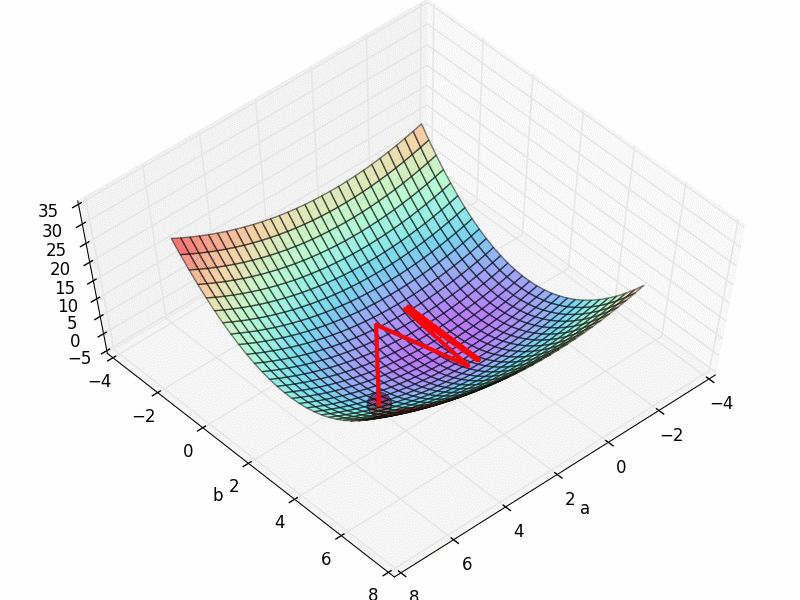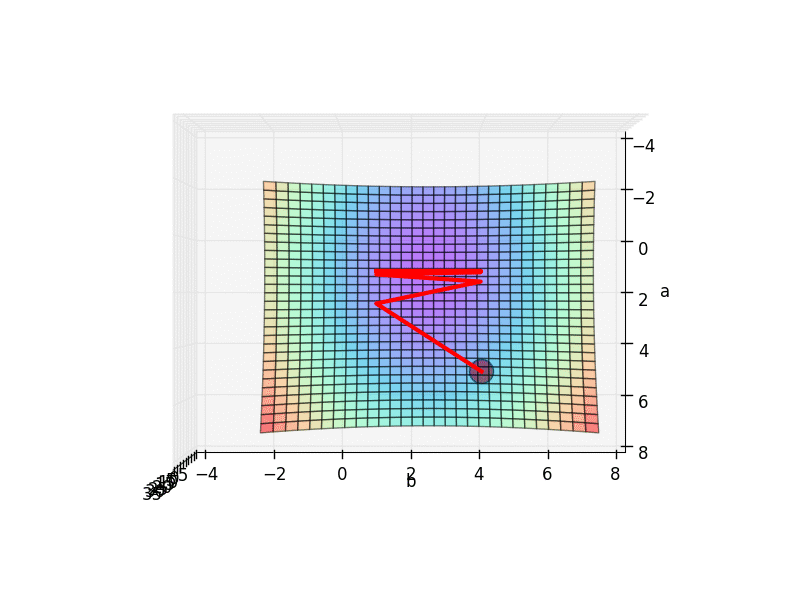
从初始的 INIT_PARAMS=[2, 4.5] 这个点开始梯度下降, 我们就能成功的找到接近全局最优的 a=1.2; b=2.5, 但是这个3D 图上有很多局部最优点, 如果我们换一个初始参数位置, 比如 INIT_PARAMS=[5, 1]. 那么就会下降到一个最靠近他的局部最优.

这样, 我们的模型就只能止步在这, 而且并不能继续向前拟合数据点了. 所以可以看出参数的初始化位置的确很重要.

通常, 在初始化神经网络的参数时, 我们可以用到 Normal distribution 等方式, 并且多做几次初始化实验, 看看效果如何. 运气好的时候, 初始化很成功, 带来的比较好的局部最优, 运气不好的时候.. 你懂的.. 继续做实验吧.