切换视频源：

Regularization 正规化

作者: Alice 编辑: 莫烦 2016-11-03

学习资料:

要点 ¶

什么是 overfitting ？

我们在用机器学习模型时，会把数据集分为训练集和测试集，训练集用来学习模型，测试集相当于新数据，用来检验模型的效果。

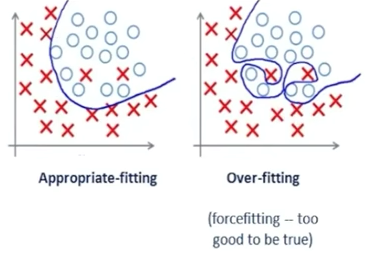
对于训练集，学习的效果非常好，甚至接近完美地穿过每个点，或者非常准确地进行了分类，但是把这个模型应用于新的数据集上，表现就特别差。这种现象叫做过拟合。

例如上图，对于训练集，左边的分类器误差比右边的大，但是处理新数据时，左边的误差就会比右边的小，因为右边太适合当前训练集的个性化了，而对普遍的规律不能进行更好地概括。

所以在实际运用时要尽量减小 overfitting。常用的方法有 L1，L2 正则化。

导入模块并创建数据 ¶

引入需要使用的Python包：

import theano
from sklearn.datasets import load_boston
import theano.tensor as T
import numpy as np
import matplotlib.pyplot as plt

数据用的是 load_boston 房价数据，有 500 多个样本，13 个 feature，每个样本对应一个房价。其中 y 通过增加维度 [:, np.newaxis] 由列表结构变成了矩阵的形式。

np.random.seed(100)
x_data = load_boston().data
# minmax normalization, rescale the inputs
x_data = minmax_normalization(x_data)
y_data = load_boston().target[:, np.newaxis]

x 因为各个 feature 的取值范围区别较大，所以用 minmax_normalization 对数据进行归一化，这样可以把每个 feature 都压缩到 0-1 的范围。

def minmax_normalization(data):
    xs_max = np.max(data, axis=0)
    xs_min = np.min(data, axis=0)
    xs = (1 - 0) * (data - xs_min) / (xs_max - xs_min) + 0
    return xs

把数据集分为训练集和测试集，交叉验证，来检验模型是否真正地学习好了。交叉验证还可以用来筛选合适的参数。

# cross validation, train test data split
x_train, y_train = x_data[:400], y_data[:400]
x_test, y_test = x_data[400:], y_data[400:]

x = T.dmatrix("x")
y = T.dmatrix("y")

建立模型 ¶

建立两个神经层，l1 有 13 个属性，50 个神经元，激活函数是 T.tanh。 l2 的输入值为前一层的输出，有 50 个，输出值为房价，只有 1 个。

l1 = Layer(x, 13, 50, T.tanh)
l2 = Layer(l1.outputs, 50, 1, None)

接下来计算 cost，第一种表达式是没有正则化的时候，会发现 overfitting 的现象。第二种是加入 L2 正则化的表达，即把所有神经层的所有 weights 做平方和。第三种是加入 L1 正则化的表达，即把所有神经层的所有 weights 做绝对值的和。接着定义梯度下降。

# the way to compute cost
cost = T.mean(T.square(l2.outputs - y))      # without regularization
# cost = T.mean(T.square(l2.outputs - y)) + 0.1 * ((l1.W ** 2).sum() + (l2.W ** 2).sum())  # with l2 regularization
# cost = T.mean(T.square(l2.outputs - y)) + 0.1 * (abs(l1.W).sum() + abs(l2.W).sum())  # with l1 regularization

gW1, gb1, gW2, gb2 = T.grad(cost, [l1.W, l1.b, l2.W, l2.b])

激活模型 ¶

定义学习率，训练函数等。

learning_rate = 0.01
train = theano.function(
    inputs=[x, y],
    updates=[(l1.W, l1.W - learning_rate * gW1),
             (l1.b, l1.b - learning_rate * gb1),
             (l2.W, l2.W - learning_rate * gW2),
             (l2.b, l2.b - learning_rate * gb2)])

compute_cost = theano.function(inputs=[x, y], outputs=cost)

训练模型 ¶

用 train_err_list 等来记录训练过程中产生的误差，方便后面可视化。训练 1000 次，每 10 步记录一次训练集和测试集的误差。

# record cost
train_err_list = []
test_err_list = []
learning_time = []

for i in range(1000):
    train(x_train, y_train)
    if i % 10 == 0:
        # record cost
        train_err_list.append(compute_cost(x_train, y_train))
        test_err_list.append(compute_cost(x_test, y_test))
        learning_time.append(i)

可视化结果 ¶

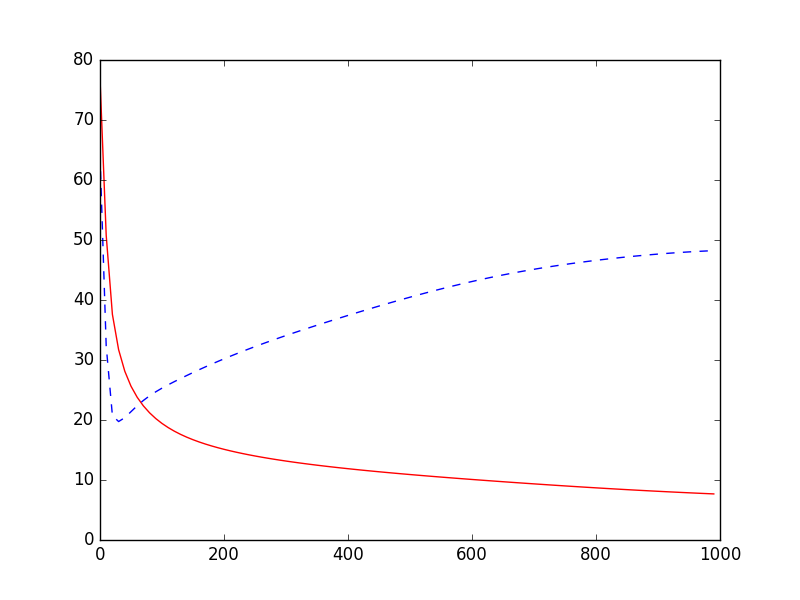
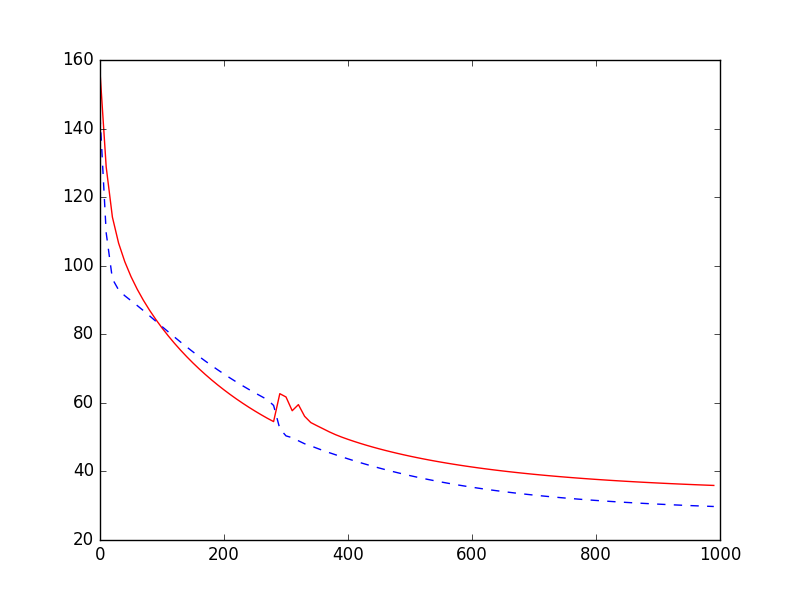
最后可视化两种误差，红色是训练集的，蓝色是测试集。

# plot cost history
plt.plot(learning_time, train_err_list, 'r-')
plt.plot(learning_time, test_err_list, 'b--')
plt.show()

没有正则化时，训练集的误差会逐渐变小，但是测试集的误差越来越大，这就是有 overfitting 。

用 L2 正则化时，比上一个好很多，测试集的误差也在不断减小。

分享到:
如果你觉得这篇文章或视频对你的学习很有帮助, 请你也分享它, 让它能再次帮助到更多的需要学习的人. 莫烦没有正式的经济来源, 如果你也想支持 莫烦Python 并看到更好的教学内容, 赞助他一点点, 作为鼓励他继续开源的动力.

支持让教学变得更优秀

点我赞助莫烦