神经网络 梯度下降

学习资料:

• 神经网络 编程教程 Tensorflow 学习目录
• 神经网络 编程教程 PyTorch 学习目录
• 神经网络 编程教程 Theano 学习目录
• 神经网络 编程教程 Keras 学习目录

欢迎观看有趣的机器学习系列视频, 神经网络是当今为止最流行的一种深度学习框架, 他的基本原理也很简单, 就是一种梯度下降机制. 我们今天就来看看这神奇的优化模式吧.

Optimization ¶

学习机器学习的同学们常会遇到这样的图像, 我了个天, 看上去好复杂, 哈哈, 不过还挺好看的. 这些和我们说的梯度下降又有什么关系呢? 原来这些图片展示出来了一个家族的历史, 这个家族的名字就是-”optimization” (优化问题). 优化能力是人类历史上的重大突破, 他解决了很多实际生活中的问题. 从而渐渐演化成了一个庞大的家族.

比如说牛顿法 (Newton’s method), 最小二乘法(Least Squares method), 梯度下降法 (Gradient Descent) 等等. 而我们的神经网络就是属于梯度下降法这个分支中的一个. 提到梯度下降, 我们不得不说说大学里面学习过的求导求微分. 因为这就是传说中”梯度下降”里面的”梯度” (gradient)啦. 听到求导微分可别后怕, 因为这个短视频只是让你有一个直观上的理解, 并不会涉及太过复杂的东西.

梯度下降 ¶

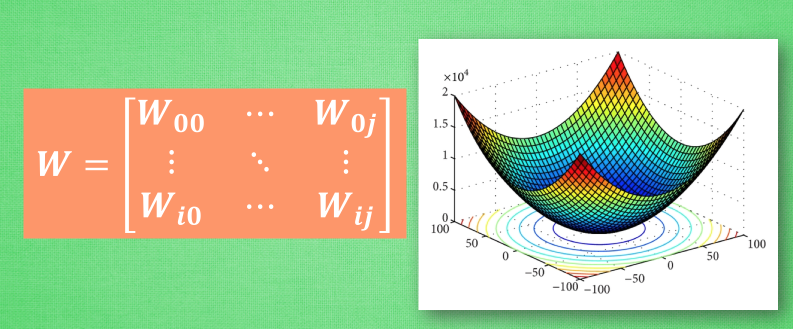
初学神经网络的时候, 我们通常会遇到这样一个方程, 叫做误差方程 (Cost Function). 用来计算预测出来的和我们实际中的值有多大差别. 在预测数值的问题中, 我们常用平方差 (Mean Squared Error) 来代替. 我们简化一下这个方程, W是我们神经网络中的参数, x, y 都是我们的数据, 因为 xy 都是实实在在的数据点, 在这个假设情况中, 是多少都无所谓, 然后我们再厚颜无耻地像这样继续简化一下, (注意, 这个过程在在数学中并不正确, 不过我们只是为了看效果), 所以现在误差值曲线就成了这样. 假设我们初始化的 W 在这个位置. 而这个位置的斜率是这条线, 这也就是梯度下降中的梯度啦. 我们从图中可以看出, Cost 误差最小的时候正是这条 cost 曲线最低的地方, 不过在蓝点的 W 却不知道这件事情, 他目前所知道的就是梯度线为自己在这个位置指出的一个下降方向, 我们就要朝着这个蓝色梯度的方向下降一点点. 在做一条切线, 发现我还能下降, 那我就朝着梯度的方向继续下降, 这时, 再展示出现在的梯度, 因为梯度线已经躺平了, 我们已经指不出哪边是下降的方向了, 所以这时我们就找到了 W 参数的最理想值. 简而言之, 就是找到梯度线躺平的点. 可是神经网络的梯度下降可没这么简单.

神经网络中的 W 可不止一个, 如果只有一个 W, 我们就能画出之前那样的误差曲线, 如果有两个 W 也简单, 我们可以用一个3D 图来展示, 可是超过3个 W, 我们可就没办法很好的可视化出来啦. 这可不是最要命的. 在通常的神经网络中, 误差曲线可没这么优雅.

全局 and 局部最优 ¶

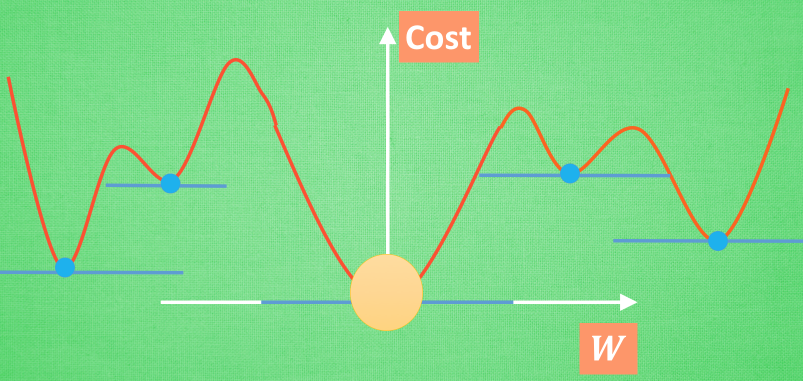
在简化版的误差曲线中, 我们只要找到梯度线躺平的地方, 就能能迅速找到误差最小时的 W. 可是很多情况是这样的, 误差曲线并不只有一个沟, 而且梯度躺平的点也不止一个. 不同的 W 初始化的位置, 将会带来不同的下降区域. 不同的下降区域, 又会带来不同的 W 解. 在这个图像当中, W 的全局最优解(Global minima)在这个位置, 而其它的 解都是局部最优(Local minima). 全局最优固然是最好, 但是很多时候, 你手中的都是一个局部最优解, 这也是无可避免的. 不过你可以不必担心, 因为虽然不是全局最优, 但是神经网络也能让你的局部最优足够优秀, 以至于即使拿着一个局部最优也能出色的完成手中的任务.

---